自由研究室

4月25日   ラテン語探検の休日　

 

 

 

 

Wikipediaに大分特産のカボスは「カブチ」「カブス」と呼ばれ、1603年ごろの日葡辞書Vocabulário da Língua do JapãoにおいてはCabusuとして説明されている、という記述がありました。　

そこでさっそくこの日葡辞書の復刻版を調べると、

Cabusu      Hum género de laranjas, ou limas

（カブス　　オレンジの一種、あるいはライム）

と説明されています。

なお、Humはumと同じで不定冠詞（男性形）

その下に次のように書いてあるようです。

Item  A árvore que de esta fruta.

（その果物のなる木）

 

さて、カブスに極めて近いラテン語にcabusという語があります。　なお、カボスとの関係はまったく分かりません。　　このcabusを例にとりラテン語の格変化を見てみましょう。　仮名を振っておきますので、読んでみてください。　ラテン語を教えに来たポルトガル人宣教師は日本人がカブスと発音するのを聞いて、「ラテン語か」とびっくりしたことでしょう。　　一方、ポルトガル語やラテン語も発音が日本語に近いですから、日本人もこれらを容易に学んでいたかもしれません。　ポルトガル語やスペイン語に日本語と同じか極めて近いものが多い事について別途まとめたいと思います。

現在のロマンス諸語は格変化が失われてしまいましたが、ラテン語では名詞、代名詞と形容詞に格変化がありました。　格変化とは「私は」「私の」「私に」のような変化です。　日本語では、てにおは（助詞）で示すところを、名詞の最後の一音節が格変化に当てられます。　まあ、そんなものかと、ご記憶ください。　

 

cabus m男性名詞 (genitive cabī); second declension　第２変化

A measure of corn　（トウモロコシの計量器）

Case                   　　　　単数                    複数

Nominative　　　主格     cabusカブス      cabīカビー

Genitive              属格      cabīカビー          cabōrumカボールム

Dative   　　　　与格      cabōカボー        cabīsカビース

Accusative　　　対格     cabumカブム     cabōsカボース

Ablative              奪格      cabōカボー        cabīsカビース

 Vocative             呼格      cabeカベ           cabīカビー

 

 

 

4月25日　今日のラテン語探検violoncello/cello e 

今日はヴィオロンチェロ（チェロ）から出発します。　

 

英語のvioloncelloは18世紀にイタリア語から英語に入ったようです。　さて、チェロは英語でもcelloと書かれますが、なぜ略号としてはVcなのでしょうか？

理由は簡単です。　celloは縮小辞だからです。

つまり、ヴィオロンチェロは⇒

ヴィオラ＋オーネ（拡大語尾）＋チェロ（縮小語尾）

ヴィオラを大きくしたもの、つまりヴィオローネ、を小さくしたもの、となります。

英語でもviloncelloと書かれることも多いです。　皆さんもこのスペルで覚えておきましょう。　また、チェロの小型のものにvioloncello piccolo があります。　これは英語でもvioloncelloのところをcelloと略さず、フルネームでvioloncello piccoloと言います。　「チェロ・ピッコロ」では縮小語が2個並んだだけで、踏んだり蹴ったりでかわいそうです。

 

✍　イタリア語の縮小辞は大変多いです。　皆さんがご存知かもしれないものを一つ挙げると

ombra （影）→　　ombra + ello（縮小辞）= ombrello 傘　　従ってombrelloは小さい影を意味します。　これが英語のumbrella アンブレラになりました。　つまり、傘はもともと日傘をさしていました。　また、縮小辞のcelloを持つものを挙げると、　campo（野原）→campicello（小さい広場）などがあるようです。　

 

この縮小時celloはラテン語の縮小時-ellusに由来するそうです。　また、ラテン語のcellaは名詞で小部屋、小区画を意味します。　このcellaを語源として、英語のcellは小さい部屋、あるいは細胞を意味します。　wine cellarワインセラーのcellarは地下室等を意味しますが、これも同じ語源と思われます。　cellセルは最小部分という意味より派生して、日本語でもいろいろな意味で使われます。　新聞やニュースで出てきたら、どういう意味で使われていたか書き留めましょう。

 

今日のまとめ　-cello’チェッロ’はイタリア語の縮小語尾、英語のcell（セル）は最小部分

 

violoncello/cello e   チェロ

violoncelle f

violoncello i

violoncelo p

violoncelo s

 

 

 

4月24日　今日のラテン語探検　

オクターブ　octave e（英語）より出発します。

 

octaveの語源についてwiktionaryにおいては From Latin octavus (“eighth”). となっています。　つまりオクターブはもともと「第8の」という意味です。

英語での「８番目の」はeighthですが、音楽でのオクターブの意味ではこのラテン語に由来する語を用いています。昨日のtri（３）もラテン語に由来するものであり、triangle等特定のものを指す時に出てくるのでした。

なお、手元の研究社の英語語源辞典では Old Frenchのoctaveからとなっていますから、英語のスペルはフランス語からのものと思われます。

 

eighth e　（8番目の） 以下の言語でottavoは男性形です。女性形では最後のoがaに変わります。

huitième f  オクターブの意味ではoctave

ottavo i　オクターブの意味ではottava

oitavo p　オクターブの意味ではoitava?　（私のポルトガル語辞書にないため分かりません。）

octavo s  オクターブの意味では octava

 

 

 

4月23日　今日のラテン語探検　　

今日はトライアングル Triangle （英語）より出発します。　

アングルが「角」だとご存知の方もいらっしゃるかもしれません。　そうすると最初の tri は３かもしれないと思われるでしょう。

Triはロマンス諸語（フランス語、イタリア語、ポルトガル語、スペイン語等、ラテン語の口語から独立した言語）において３を意味する接頭辞です。

次のangleはフランス語において角（かど）を意味します。　つまり、Triangleはフランス語において三角、あるいは三角形という意味です。

英語の３はthreeですが（これはゲルマン語派の言葉であり、ラテン語に由来しません。）　、三角形あるいはトライアングル（打楽器）と言う時は、フランス語からtriangleがそのまま使われます。

 

英語はこの様に、ゲルマン語派の言葉以外にラテン語・ロマンス語の言葉が頻繁に使われています。　　

 

Wiktionaryには次のように説明されています。

Triangle  (English)

From Old French triangle, from Latin triangulum, noun use of adjective triangulus (“three-cornered, having three angles”), 

from trēs (“three”) + angulus (“corner, angle”).

古フランス語Old Frenchのtriangleから、ラテン語のtriangulum = trēs (3) + angulus (角)と説明されています。

 

 Triangle e

Triangle f

triangolo i

Triângulo p

Triángulo s

それぞれの言語で「３＋角」となっています。

f フランス語、i イタリア語、p ポルトガル語、s スペイン語

 

なお、音楽ではトリオ、オクターブ等ラテン語（ロマンス語）の数に由来するものがいくつもあります。　今後探検しましょう。

 

✏　このOld Frenchは9世紀から14世紀ごろまで北フランスで話された言葉です。　　

従って、11世紀のノルマン・コンクエストの時にイギリスに大量に流入したフランス語はこの古フランス語です。　このため、英語のラテン語由来の言葉の多くは、このように「古フランス語から」となっています。

 

 

 

 

 

普段、私たちが使っている言葉や、中学、高校までに英語や音楽等で出てくるラテン語起源の言葉とラテン語の直接の子孫の言葉を拾ってみましょう。

　現在、ラテン語を公用語とする地域はバチカン市国だけにしまったようですが、古代ローマ帝国ではラテン語が公用語でした。　左の図は西暦３９５年の東西分割統治時のローマ帝国の領土を示します。　この様にローマ帝国内が広いので文書は統一されていても、言葉はかなり違っていたと言われています。　そのいくつかの方言が独立した言語となり、今日のポルトガル語、スペイン語、フランス語、イタリア語、ルーマニア語等となっています。　また、カタルーニャ語、プロヴァンス語も同様にラテン語の直接の子孫です。　これら直接の子孫をロマンス語と言います。　政府の公文書でなく、ロマンス（小説）を書くのに用いられたためと思います。　これらの言語では日常生活で用いる単語にいたるまでほとんど共通です。　文法もほとんど同じです。　ただ、例えば名詞においては、いくつかある意味のどれを普段用いるか、また動詞においては過去を言うときに動詞自身が過去用に変化する単純形か、過去分詞を用いた複合形か、と言った様な違いがあります。　これに対し英語等のゲルマン系の言語は同じヨーロッパの言語でありながら、日常単語は異なり、文法もある程度異なっています。

　そこで、日常使っている言葉や中高で習う言葉の内、ラテン語とロマンス語の言葉だけについて説明を試みようというものです。

 

　以下、順不同ですがご了承下さい。　今後、追記したいと思います。　

 

　まず、英語の歴史に大転換となったノルマン・コンクエストから始めたいと思います。　ラテン語の直接の子孫でない英語から始めるのは変だと思われる方もあると思いますが、英語にフランス語が大量に導入された大事件ですので、これは見逃せません。　

 

言語についての略号は次の通りです。英語については多くの場合このeを省略しました。

L ラテン語

e 英語

i スペイン語

p ポルトガル語

s スペイン語（カスティーリャ語）

 

 

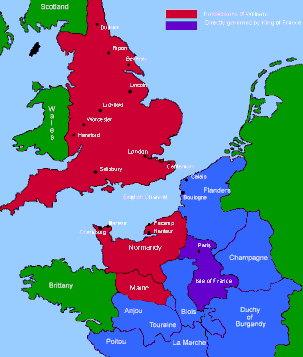
　(フランスに住む)ノルマン人のイングランド征服という意味です。　ここで言うノルマン（北の人）という言葉はラテン語でなく、ゲルマン系の言葉であり、フランスから見て北の人、もともとはおそらくスカンディナヴィアの人を指したものと思います。　現代のフランス語でnormand(e)は「ノルマンディーの（人、もの）」を意味します。

 

フランスのノルマンディー公ウィリアムがイングランドの王位継承権を主張して1066年、イギリスへ攻め入り、英国王ハロルドは敗れて，ノルマンディー公がイングランド王を兼ねることになりました。このがノルマン・コンクエストです。　左図の赤いところが支配地域です。

　今日、英語には膨大な量のフランス語が流入していますが、この最大の原因はノルマン･コンクエストです。　ノルマン・コンクエスト以降イギリスでは支配階級にてフランス語が使われるようになりました。　これは１００年戦争を経て、イギリスとフランス間の国境が決まるまで続きました。　また、フランス語からの流入はその後も続き現代にいたります。　ノルマン・コンクエスト以前の英語(old English)はラテン系の言葉を含まず、北欧語のようにまったくのゲルマン系の言葉でした。　これに対して、ノルマン・コンクエストからおおよそ15世紀ごろまでの英語をmiddle Englishと呼びます。この時代の英語で書かれたものの代表はジェフリー・チョーサーのカンタベリー物語でしょう。　なお、シェークスピアの文章は現代英語を知る人でもなんとか読める事が多いが、この時代の英語はearly modern Englishと呼ばれています。

 

 

✎ Great Britainとは

フランスにブルターニュ半島あるいはBretagne地方がありますが、海を越えた向こうにもっと広い大地があります。　フランスではこれをLa Grande-Bretagneと呼びました。　これをそのまま英語に訳すとGreat Britainとなります。　Great Britainは以前、大英帝国と訳されたことがありましたが、もともと偉大なブリテンのような意味ではありません。　それに王国ですからあまり適訳ではないでしょう。　今日でも英語でBritain（イギリスあるいは北アイルランドを除くイギリスのブリテン島の部分）と言うところをフランスではGrande-Bretagneと言っています。　私事ですが、昔イギリスで印刷されたフランス語の本を見たらImprimé en la grande-bretagneと書かれていてびっくりしたものです。

 

 

 

マグナ・カルタはよく次のように説明されています。

 

１２１５年、イギリス王ジョンに対し、貴族と都市が王権の制限、貴族の特権、都市の自由などを認めさせた文書。 「法による支配」などの立憲主義の出発点であり、イギリス憲法の一部と位置づけられている

 

Magna Carta Libertatum は次の意味です。

magnus（重大な）

+ carta（パピルス、パピルスから作ったもの、手紙）

+ libertatum （自由の）

 

このcartaは各国に同じスペルで現在まで使われています。　　

ここではcartaについて、各言語での4番目までの意味を一覧にします。　スペイン語、ポルトガル語では今でも手紙、文書の意味で用いられます。　

 

イタリア語carta 

現代のイタリア語ではcartaは次の通りの意味です。　手紙の意味ではlettera（文字、手紙）が用いられます。

1. paper (the material材質としての紙、bicchieri di carta紙コップ)

2. map（地図）

3. menu（メニュー）

4. card（カード）

ポルトガル語carta 

1. letter (written message書かれたメッセージ、文書)

2. chart, map (visual representation of an area地図)

3. (card games) playing card (any of the 52 rectangular pieces of card used to play games日本のカルタの語源はこのポルトガル語だと言われています。)

4. (law) charter (document issued by some authority, creating a public or private institution, and defining its purposes and privileges憲章、特許状)

スペイン語carta f (plural cartas)

1. letter (document)

2. map

3. menu (list of dishes in a restaurant)

4. playing card（カード）

フランス語carte 

1.    地図 

2.    カード

3.    札 

4.    メニュー 

 

 

 

レコンキスタ　reconquista (p/s) は

re（再び）+ conquistar（征服する）より作られたものだと思います。

コンキスタドール　conquistador (s)

どちらもスペイン語のconquistar（征服する）より作られたものです。　conquistarの語源はラテン語のconquisitō（征服する）です。

 

なお、私のスペイン語の辞書ではどちらも普通名詞でした。　ここでは普通名詞として小文字で始めました。　もしかするとポルトガル語ではこの歴史上の意味では固有名詞なのかもしれません。　また、以前イギリスの高校の教科書を見た時、レコンキスタは単にreconquest（再征服）、コンキスタドールはconqueror（征服者）と普通名詞になっていました。

 

 

 

ルネサンスRenaissance (e/f)

これはもともとフランス語ですが、同じスペルで英語でも用いられます。

「re再び + naissance 生まれる事」であり、14世紀にイタリアで始まり、西欧各国に広まったギリシャ・ローマの文芸を復興するもの、という意味です。　なお、この語は19世紀に初めて使われました。

このnaissanceは誕生です。　その動詞naîtreはラテン語のnāscīよりフランス語化したものです。　このナあるいはネの音で始まる語が生むに関係しているものが多い事を覚えておいてください。　次にいくつかnaissanceに関係してナやネで始まる語を見てみましょう。

 

Nation (e/f)

これはnaで始まりますから、第一義にはそこで生まれた民を意味します。

第二にその民の国家という意味で使われます。　

 

Nature (e/f) Natura (i)

これは日本語で言うところの自然（人工物のない様子）とはあまりにも違います。　-turaはラテン語の未来分詞の一つを作る語尾です。　従って、naturaは生むであろうもの、またそれによって生まれたものという意味です。　ヨーロッパの方がNatureや/Naturaと言うときは、私たちや地球上のすべてのものを生み出すものという意味を含んでいると思います。　だからNature/Naturaを大事にしないといけないと言っている事もあるでしょう。

 

 

naïf/ve (f)（男性形/女性形）ナイーブ

これも「生まれる」から生じた形容詞です。（ラテン語nativus）　従って基本的には、生まれたままの、うぶな、世間知らずの、未経験のという意味です。　人に使うときは注意が必要です。　英語ではnaiveと綴られ、基本的には同じ意味だと思います。　例を挙げましょう。

naive ideas甘い考え

He is naive about~.　　彼は～について分かっていない、未経験だ。　

 

 

✎ naïfのïはフランス語のアクサンの一つでtrémaと呼ばれます。　フランス語でaiと綴るとエのように発音されます。　そうでなく文字通り、これをアイとして読む時にïと書く必要があります。

 

 

ラテン語の接尾辞を２つ見てみましょう。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

一つ目は　-ia　これは場所を表す接尾辞です。

例を挙げると次の通りです。

他にもたくさんあります。

 

Oceania (e/i)：ocean+iaで、オセアニア「大洋州」

Germania (i)　ゲルマン人の地　ドイツ

Bulgaria (e/i/s)　 Bulgar +‎ -iaブルガール人の地　ブルガリア

Micronesia (e/i/s) (mikrónēsos小さな島) +‎ -ia　小さな島の地域

新しいところではアメリカのペンシルバニア州があります。

Pennsylvania (e) 　Penn (ウィリアム・ペン)-sylva（森）- ia　　

もともとは「ペンの森の地」の様な意味です。　

✎　William Penn (1644- 1718)　ペンシルバニア植民地総督

 

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

二つ目は-logyです。

-logyとは、～を論じる事、～学の意です。

普段使う語としてはorologio (i)   horloge (f) 時計があります。

 

つまりorologioは(ora)をlogio（言う）、つまり時を言うものなのです。　 

直接の語源はhōrologium (L)です。

 

さて、wikipediaによれば、logyは、ギリシア語のλεγειν（話す）という動詞から派生した名詞λόγος（ロゴス）に接辞の-ίαがついたλογία（ロギア）からとなっています。　従って、～学、～論という意味です。　この様なギリシャ起源の学問用語の多くはラテン系の言語において男性名詞となります。　　

ロゴマークのロゴ、ブログのログも同じ語源です。　ロジックも同じ語源だと思います。

各言語によって次のように綴られます。

–logie (f)

-logía (s)

-logia (L/i/p)

音楽学を例にとると、次の通りとなります。

musicology (e)

musicologia (i/p)

musicología (s)

 

以下、英語のスペルでlogyの付くものを挙げてみましょう。　

 archeology　考古学

biology　生物学

psychology　心理学

theology　神学

iconography　図像学

sociology　社会学

ecology　環境学　「エコ」はここからきていると思います。

etymology　語源学

ieology　イデオロギー

geology　地学

mythology　神話学、神話全体

zoology　動物学

 

 

 

 

英語のminute は形容詞としては（名詞と異なる読み方で）「微小な」という意味をご存知の方も多いしょう。　ここではイタリア語でsecondoが出てくるまでの道のりを確認しましょう。

１時間の60分の一を第一の微小部分としてminuto primoとしました。minuto primoは単にminutoとも言われます。　その１分の60分の1を第二の微小部分として、minuto secondoとしました。　これを略してsecondoとも言われます。　正確に言えば、第二の微小部分が出てきたので、第一の微小部分と言わなければならなかったのでしょう。

 

ora = 時間

minuto primo = 第一の微小部分　（分）　minutoと略されます。

minuto secondo = 第二の微小部分（秒）　secondoと略されます。

 

 

 

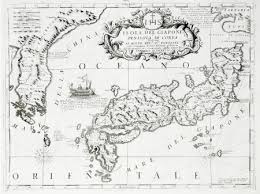
左の地図はIsola Del Giapone Penisola Di Corea（日本の島と朝鮮半島）と題された地図です。

isola =　島

penisola = 半島 

From Latin paenīnsula (“peninsula”)

paene (“almost”) + īnsula (“island”).

従って、pen + isolaで「ほとんど島」という意味です。

このpenのところは印欧祖語に由来する古い言葉だそうです。　ただ、他にこの意味のpenで始まる例が見当たりません。　どなたかご存知の方がいらっしゃいましたらお知らせください。

 

 

 

 

自由研究 Meantone ミーントーン

 

　自由研究 1 音階と数学　において、音階は周波数で見ると等比数列で表されることを見ました。　平均率では純正な和音はオクターブしかないのでした。　それ以外は1.0594631··を掛けて求めるのでした。　また、平均律では5度（ド→ソ等）、4度（ソ→ド等）は純正な和音に近いですが、3度（ド→ミ等）は大きく異なるのでした。　注意；5度は半音7個分であることを確認しましょう。

 

さて、「自由研究 1 音階と数学」の最後のページに、平均律でない例としてミーントーンを挙げました。

ここではこのミーントーンの考え方を見てみましょう。　今回も数学の話となります。

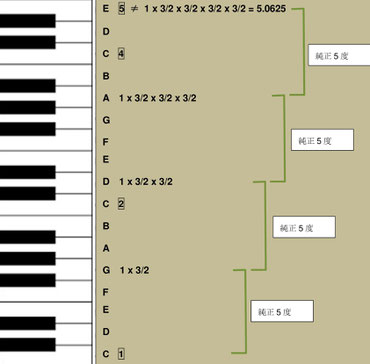
上の図は、2オクターブと3度の音域を持つ鍵盤です。　鍵盤のすぐ右にCDEFGABと音名が書かれています。　そのすぐ右に四角で囲った数が下から、1, 2, 4, 5と書かれています。　これは一番下のドを1とした時の周波数の比を示しています。　1, 2, 4はオクターブの関係にありますから調律法に関係なくこの様に整数で表せます。　次の5は 4（すぐ下のド）に対して次の計算より求めたものです。

4（すぐ下のド） x 5/4（純正長3度） = 5

となります。　つまり、この5は4（ド）に対して純正長3度上のミを与えるものです。

一番下のドから5度上のソ、その5度上のレ、その5度上のラ、そして、その5度上のミをこの鍵盤上で確認しましょう。　もし、この5度を純正5度とすると、純正5度は3/2で表せますから、ミはこの図のように、

1 x 3/2 x 3/2 x 3/2 x 3/2 = 5.0625

となってしまいます。　

さて、この3/2 ＝ 1.5をほんの少し小さくして、4回掛け合わせて、ちょうど5にできるでしょうか？

これを5の4乗根と呼び、⁴√5 と書きます。　

^{また、Formula 2    4}√5 = 1.495348781···    irrational number

であることが分かっています。　irrational numberは比で表せない数という意味ですが、無理数と訳されているのでした。　電卓等でこれを4回掛け合わせていくつになるか確かめてください。

これがミーントーンを決定付ける数です。　これも無理数ですからピッタリ5にはならないと思います。　

以下、下記リンクよりclavichord-laboratoryへ進んでください。　英文の説明となります。　中学レベルの文法を用いたつもりですが、不正確なところがあればお知らせください。　また、ところどころ、クラヴィコードを設計するために周波数から実際の弦長を求めています。　この部分は参考までにご覧ください。　なお、'speaking length'は振動する弦の長さを意味します。　　

 

https://virginalclavichord.jimdofree.com/clavichord-laboratory/

 

なお、音名はこの中ではCDEFGAHとドイツ式になっています。　この点をご了承下さい。

 

また、「自由研究 1 音階と数学」でもみましたが、円周率だけでなく、いろいろなものが、無理数となります。　自転車や電車を設計する時にも、無限に続く数を扱えません。　そこで小数以下、何桁計算すれば十分な精度となるかが重要となります。　

 

序　 等差と等比　（数学入門）

 

◇ 等差

 

　　１階から階段を上って２階へ行くとき、あまり段差を意識していないと思います。　どうして一段一段、確認しないのでしょうか？　それは段差が一定だからです。　

この１段あたりの段差は、小学校では１６㎝（センチメートル）以下、中学では１８㎝以下と決まっています。　

一般住宅内ではもう少し段差が大きくなり、２０㎝くらいとなります。

１階の高さを０㎝とすると、階段を一段上がると

２０ｃｍの高さとなります。　もう一段上がると４０㎝の高さとなります。

この様に、一段上がるごとに２０㎝づつ高くなっていきます。　１２段目でだいたい２階の高さとなります。

 

 

12段目の高さ           240㎝

11段目の高さ           220㎝

10段目の高さ           200㎝

9段目の高さ             180㎝

8段目の高さ             160㎝

7段目の高さ             140㎝

6段目の高さ             120㎝

5段目の高さ             100㎝

4段目の高さ             80㎝

3段目の高さ             60㎝

2段目の高さ             40㎝

1段目の高さ             20㎝

一階の高さ　             0㎝

 

 

ここに0から240までの数字が並んでいます。　この様な数字の列を数列(progression/ progression of mathematics)と呼びます。

また、隣同士の高さの差は20ですから、「等差である」と言います。　また、この数列を等差数列 (arithmetical progression)と呼びます。　皆さんが、階段を一段づつ確認しなくても上がったり下りたりできるのは、段差が等しいからに他なりません。

 

 

　皆さんのお小遣いが今年の1月に1000だったとしましょう。　毎月100円づつこのお小遣いが増えるとしましょう。　来年の1月には2200円となります。　これも等差数列です。

 

2020年

1月    1000円  

2月    1100円 

3月    1200円 

4月    1300円

5月    1400円

6月    1500円

7月    1600円 

8月    1700円 

9月    1800円 

10月  1900円

11月   2000円 

12月   2100円               

                                                                                                                                                                  2021年

1月

2200円

 

「等差である」とは、このように隣り合ったところでは差が常に一定であるという意味です。

 

 次は等比について考えましょう。

 

 

 

 

◇ 等比I　入門編

 

等差に対して等比があります。　もっとも身近な比は消費税かもしれません。　消費税は現在10パーセントです。　購入するものの値段と消費税を合わせて1.1倍のお金を支払うことになります。　　

 

100円のものを買うと

100 x 1.1 = 110円と支払います。

10000円のものを買うと

10000 x 1.1 = 11000円となります。

 

つまりいつも支払う額はものの価格に1.1を掛けたものです。

この1.1は高いものを買うときも、安いものを買うときも変わりません。

この計算するのが面倒だから、消費税を一回100円と決めたらどうなるでしょう。

そうすると100円のものを買うのに100円の消費税を加えて200円支払わなければなりません。

また、10000円のものを買うときも100円の消費税とすると、支払額は10100円となります。

また、100円のものが100個入った一ケース10000円のものも消費税は100円だとすると、まとめ買いがお得、となります。　1000万円で家を購入する時も消費税は100円、50円の消しゴムを買うときも消費税は100円とすると、不公平であり、また日々の生活に支障があります。

 

これを解決するのが、ある一定の比を掛ける、つまり価格に1.1をかけて支払額としています。　これだと、高いものを買う人はそれなりに税を負担しているので公平でしょう。

このように比と言う概念は身近なものです。

 

さて、1月に1000円だったお小遣いは変わりませんが、次の月から、お小遣いが1.1倍になるとしましょう。

皆さんは、お小遣いが毎月100円上がるのと毎月1.1倍になるのとではどちらが良いですか？　

お小遣いが毎月1.1倍となる様に、隣り合ったものの比が一定である場合、「等比である。」と言います。　また、下記のように隣り合った数が等比の数列を等比数列 (geometrical progression)と呼びます。　今年の1月に1000円だったお小遣いはどのように増えていくでしょうか？　（少数点以下を切り捨てています。）

 

 

2020年

1月

1月　1000円

2月　1100円

3月　1210円

4月　1331円

5月　1464円

6月　1610円

7月　1771円

8月　1948円

9月　2143円

10月　2357円

11月　2593円

12月　2853円

 

2021年

1月　3138円

2月　3452円

3月　3797円

4月　4177円

5月　4574円

6月　5054円

7月　5559円

8月　6115円

9月　6727円

10月　7400円

11月　8140円

12月　8954円

 

2022年

1月　9849円

2月　10834円

3月　11918円

4月　13109円

5月　14420円

6月　15863円

7月　17449円

8月　19194円

9月　21113円

10月　23225円

11月　25547円

12月　28102円

 

2023年

1月　30912円

 

 

毎月お小遣いが1.1倍になるとすると、3年後には1000円だったお小遣いが3万円になってしまいます。　

驚いた方はいますか？　「これに驚いた方は、一生借金をしてはいけません！」　借金はこのように増えるものだからです。　借金に限らず等比のものは世の中にとても多く、値が急速に大きくなるので注意を怠ってはいけません。　等比とは山火事の様なものです。　

「等比というのは刻々と燃え広がる山火事を実況中継する様なイメージです。」　

　

さて、ある音の高さは周波数（振動数）で表されます。　ㇻの音が440Hzだとご存知の方があるかもしれません。　　チェンバロやピアノのベントサイド（奏者に対して右側面）がカーブしているのは、基本的に半音低くなるごとに等差ではなく、等比で弦が長くなっていくからです。　

 

次はいよいよ数学らしい考え方が登場します。　難しくはありません。　よく考えてみましょう。